Ступени звукоряда будем располагать в диапазоне фортепиано. Все-таки клавишные инструменты одни из самых распространенных, чего стоит только электронный синтезатор, который сейчас по цене доступен практически каждой семье.
Уроки музыки. Звукоряд. Часть 2.
Ступени звукоряда. Начинаем построение.
С чего начнем? Предлагаю начать с уже имеющегося. Мы имеем звук с частотой 440 Гц.
| Он выбран не случайно. Этот звук находится в очень удобном месте звукового диапазона. Во-первых, его могут пропеть люди с разными голосами. От самого низкого мужского баса, до самого высокого женского колоратурного сопрано. Во-вторых, музыкальные инструменты делаются так, чтобы они могли аккомпанировать пению и их диапазон близок к певческим голосам. Поэтому звук на 440 Гц могут воспроизвести очень многие музыкальные инструменты. |
Будем умножать/делить частоту 440 Гц на 2, чтобы получать сливающиеся звуки до тех пор, пока не выйдем за диапазон фортепиано. В результате получим ряд значений звуковых частот:
| 27,5Гц | 55Гц | 110Гц | 220Гц | 440Гц | 880Гц | 1760Гц | 3520 |
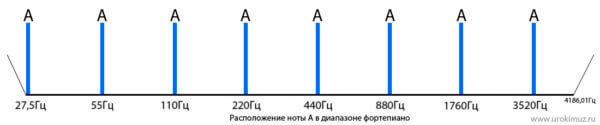
Первая нота на звукоряде
Разместим эти частоты в диапазоне фортепиано:
Так как это первый звук, который мы поместили на звукоряд, назовем его латинской буквой А.
То, что получилось много звуков с одинаковым названием вполне нормально — все эти звуки сливаются на слух. По сути, это одна и та же нота, только звучит на разных частотах.
| С высоты «космического века» мы сильно упрощенно смотрим на деятельность музыкантов в прошлом. Например, мы с легкостью употребляем такие понятия как частота, колебания в треть или четверть длины струны и тому подобное. Музыканты в давние времена никаких «герцев» не знали и до всего рассказанного выше им пришлось доходить в процессе поиска и экспериментов. Пробовались разные конструкции музыкальных инструментов, которые издавали требуемые звуки. Работа вначале шла с инструментами с диапазоном в 1 — 2 октавы, а до фортепиано человечество дошло через тысячи лет развития музыки. |
Сделаем вывод:
на звукоряде располагаются периодически повторяющиеся ноты.
Продолжим наполнять звукоряд другими звуками.
Возьмем струну равную 1/3 длины эталонной струны. Частота колебаний такой струны равна:
440 х 3 = 1320 Гц
Найдем для частоты 1320 Гц сливающиеся звуки. Для этого умножим и поделим её на 2.
Получим новый ряд звуков:
| 41,25Гц | 82,5Гц | 165Гц | 330Гц | 660Гц | 1320Гц | 2640 |
Расположим эти звуки на звукоряде. Для удобства на рисунке покажем не весь диапазон фортепиано, а его более узкий участок:
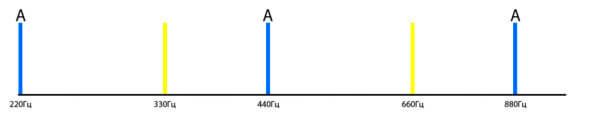
Вы уже поняли, как можно найти частоты музыкальных звуков для заполнения музыкального звукоряда? Берем какой-то обертон эталонной струны и для этого обертона находим сливающиеся звуки.Конечно, не каждый обертон ляжет в звукоряд, но принцип заполнения звукоряда должен стать понятным.
Для закрепления проделаем расчет частот еще одного звука в музыкальном звукоряде.
Возьмем струну равную 1/17 части длины эталонной струны. Частота колебаний такой струны равна:
440 х 17 = 7480 Гц
Для фортепиано это слишком высокий звук, поэтому сразу уменьшим его на 2 и получим частоту 3740Гц.
Найдем для частоты 3740 Гц сливающиеся звуки. Для этого умножим и поделим её на 2.
Получим новый ряд звуков:
| 58,4375Гц | 116,775Гц | 233,75Гц | 467,5Гц | 935Гц | 1870Гц | 3740Гц |
Расположим эти звуки на звукоряде.
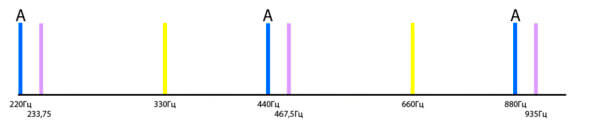
Дабы не утомлять вас числовыми расчетами, разместим на звукоряде основные звуки (ступени звукоряда), которые можно получить работая с частями (обертонами) эталонной струны:
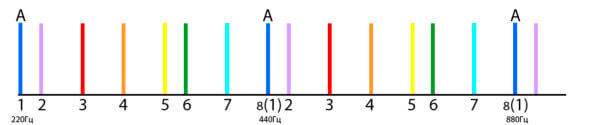
Всего получилось семь основных звуков.
| На рисунке они обозначены разными цветами и пронумерованы. Частоты не указаны. Почему? Станет понятно позже, а сейчас скажем, что до сих пор мы имели дело с частотами, которые издают реально существующие в природе предметы (мы говорили о струнах). Эти частоты можно получить, если делить «первоначальную» струну на 2, 3, 4, 5, 6 и более частей. Звукоряд в музыке составленный из таких реально существующих частот называют натуральный звукоряд. |
При продвижении по звукоряду можно заметить, что с каждого восьмого звука происходит повторение семи основных звуков. Восемь на латыни — октава. Именно так назвали восемь основных музыкальных звуков подряд. Восьмой звук октавы является первым звуком следующей октавы.
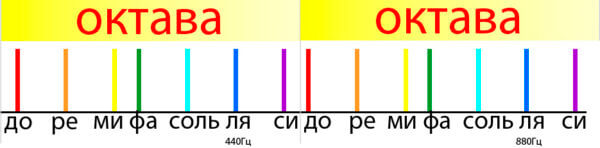
На рисунке звуки подписаны названиями нот (до, ре, ми, …) откуда они произошли читайте на следующем занятии.
Перейти на Уроки музыки. Звукоряд. Часть 3. Ноты звукоряда
Если в статье нашли для себя что-то полезное, поделитесь с друзьями. Нам это действительно нужно и мы будем еще лучше работать для вас:
Кто желает научиться играть на каком-либо духовом инструменте, например, поперечная флейта, рекомендуем взять в помощь программу Свирелька: